
ーーーーーーーーーーーーーーーーーーーーー
- 試験前なのに電気回路のことがわからない。
- 大学で学ぶ電気回路の基礎を知りたい
- 電気・電子系の学部に入ったけど具体的に何をするのかわからない
ーーーーーーーーーーーーーーーーーーーーー
そんな悩みを持つ大学生や高校生の皆様に向けて、今回はRC直列回路という電気回路を扱う上で最も基礎的な回路例に回路の微分方程式を立てて解くという一連の流れを丁寧に解説します!最後に例題も載せているので演習問題としてぜひご活用ください。
RC直列回路とは
まず、RC直列回路について解説します。RC直列回路とは以下のような回路図であらわされる回路のことを言います。ここでは電圧源は乾電池などの直流電源で電圧はV[V]、抵抗値はR[Ω]、コンデンサはC[F]とします。また、出力電圧はコンデンサにかかる電圧$$ V_C $$[V]とします。出力電圧とは取り出したい電圧のことです。
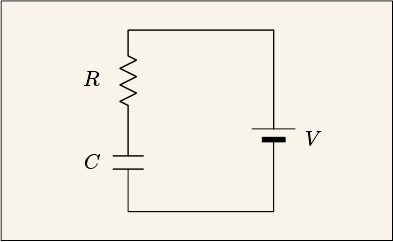
結論から言うと、出力電圧は、
$$
V_C(t) = V\left(1 – \mathrm{e}^{-\frac{t}{RC}}\right)
$$
と表すことができます。また、このグラフは以下の通りです。
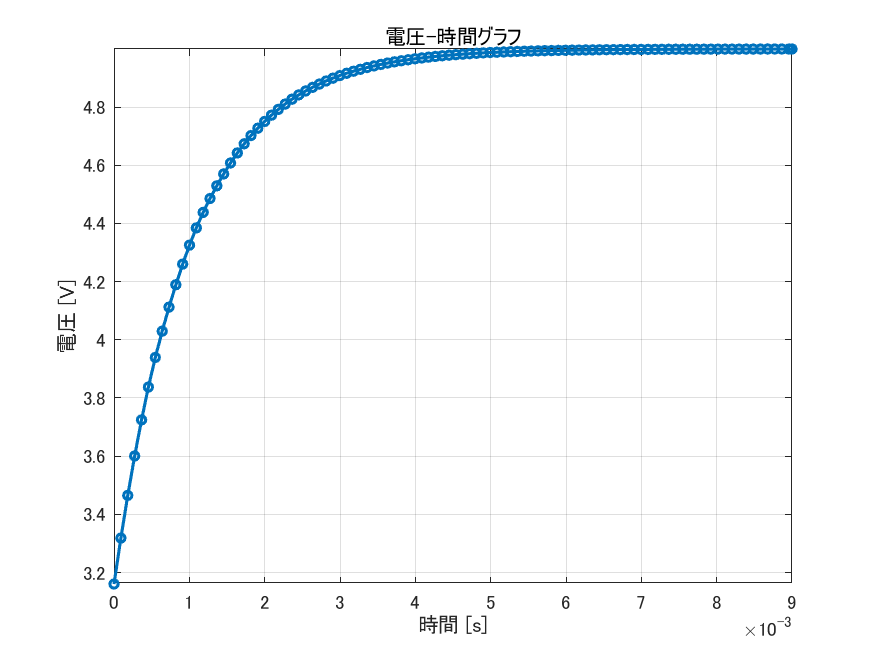
このグラフからわかる通り、初めはコンデンサの電圧は0Vですが、時間とともに増加していき、おおよそ5秒でフル充電されることがわかります。この結果を数式を用いて導出していきましょう。
微分方程式の立て方
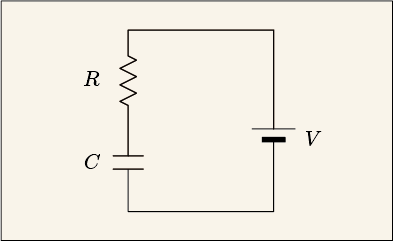
まず、抵抗とコンデンサが直列につながれているので流れる電流はどちらも同じです。では、どれくらいの電流が流れるのかを調べます。コンデンサには
$$
Q = C V_C
$$
つまり、蓄えられる電荷は電圧に比例するという関係がありました。電流は電荷の時間変化を表す量なので、電荷を時間で微分すると電流になります。すなわち、
$$
i(t)=C\,\frac{dV_C(t)}{dt}
$$
という式が導出できます。また、抵抗にかかる電圧は、
$$
V_R = R i(t)
$$
と表されます。回路を一周した後の電圧の変化は結局 0 V なので、
$$
V_R + V_C = V
$$
が成り立ちます。この式に先ほどの2つの式を代入すると、
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = V
$$
という微分方程式を導出することができました。
微分方程式の解き方
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = V
$$
この微分方程式を解くためにはまず
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = 0
$$
の微分方程式を解けないといけません。
両辺をRCで割ると、
$$
\frac{dV_C(t)}{dt} + \frac{1}{RC} V_C(t) = 0
$$
です。移行すると、
$$
\frac{dV_C(t)}{dt} = -\frac{1}{RC} V_C(t)
$$
変数分離して、
$$
\frac{1}{V_C(t)} dV_C(t) = -\frac{1}{RC} dt
$$
これの両辺を積分すると、
$$
\log\bigl|V_C(t)\bigr| = -\frac{t}{RC} + A
$$
です。ここで、Aは積分定数とします。この式を変形すると、
$$
V_C(t) = A \mathrm{e}^{-\frac{t}{RC}}
$$
とできます。
一般に、
$$
(\frac{d}{dt} + A) x(t) = 0
$$
という微分方程式の解は
$$
x(t) = B \mathrm{e}^{-At}
$$
と表すことができます。ただしAとBは定数です。この微分方程式の解は何度も出てくるのでこのまま覚えてしまいましょう!
最後に、
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = V
$$
を解いていきましょう!といっても、先ほどの解$$ A \mathrm{e}^{-\frac{t}{RC}} $$に帳尻合わせで何か定数を足してあげるだけです。なぜそれでオッケーなのか?それは、解きたい微分方程式の右辺が定数だからです!よって、解を
$$
V_C(t) = A \mathrm{e}^{-\frac{t}{RC}} + B
$$
と表すと、Bは定数なので微分したら0だから、
$$
B = V
$$
とわかります。以上から、微分方程式の解は、
$$
V_C(t) = A \mathrm{e}^{-\frac{t}{RC}} + V
$$
です!
また、初期条件を$$ V_C(0) = 0 $$ と仮定すると、
$$
A = -V
$$
なので、
$$
V_C(t) = V\left(1 – \mathrm{e}^{-\frac{t}{RC}}\right)
$$
が導けます!
例題
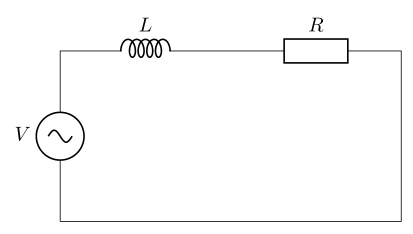
RL直列回路について考えます。電圧源はV [V]の直流電圧源とします。
【解答】
直列なのでコイルにも抵抗にも同じだけ電流が流れます。その値をi(t)とします。
コイルでの電流と電圧の式は、
$$
V_L(t) = L\frac{di(t)}{dt}
$$
だから、
$$
V_L + Ri = V
$$
に代入して、
$$
L\frac{di(t)}{dt} + Ri(t) = V
$$
これを解くと、
$$
i(t) = A \mathrm{e}^{-\frac{R}{L}t} + \frac{V}{R}
$$
初期条件を、i(0) = 0とすると、
$$
i(t) = \frac{V}{R}
(1 – \mathrm{e}^{-\frac{R}{L}t})
$$
とわかります。今求めたいのはコイルにかかる電圧なのでもう一度
$$
V_L(t) = L\frac{di(t)}{dt}
$$
に代入すると、
$$
V_L(t) = V \mathrm{e} ^ {\frac{R}{L}t}
$$
とわかります。これが答えです。

コメント