
ーーーーーーーーーーーーーーーーーーーーーーーー
- 試験前なのに電気回路のことがわからない。
- 大学で学ぶ電気回路の基礎を知りたい。
- 電気・電子系の学科に入ったけど具体的に何をするのかわからない。
ーーーーーーーーーーーーーーーーーーーーーーーー
そんな悩みを持つ大学生や高校生の皆様に向けて、今回はRC直列回路という電気回路を扱う上で最も基礎的な回路例に回路の微分方程式を立てて解くという一連の流れを丁寧に解説します!
このページでは、
・定数変化法を用いた1階非同次微分方程式の解き方
・交流電圧源があるときのRC直列回路の解き方
がわかります。また、『RC直列回路からわかる微分方程式の解き方』の続きになっています。RC直列回路に直流の電圧源がある場合の解き方がわからない方はこちらをご覧ください。
まずは、最終的な結論を述べます。この回路の微分方程式を解くと、答えは
$$
V_C(t) = \frac{wRC}{\sqrt{1 + (wRC)^{2}}} V \mathrm{e} ^{-\frac{t}{RC}} + \frac{V}{\sqrt{1 + (wRC)^{2}}} \sin(wt + \phi)
$$
となります。何を言っているのかさっぱりですよね。でも、これをグラフにすると納得いくと思います。グラフは、以下のようになります。
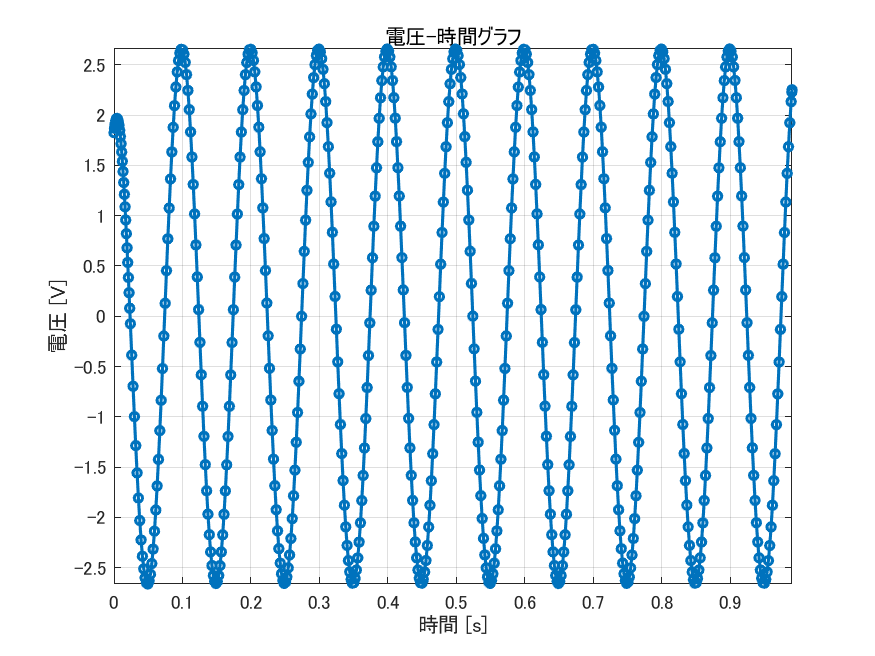
つまり振動するわけです。どうしてこうなるのか、微分方程式を解くことで解析していきましょう。
【復習】RC直列回路の微分方程式
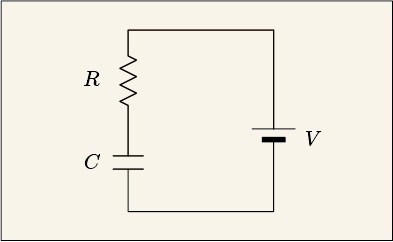
この回路の微分方程式は、
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = V
$$
という風に書けました。では、この電圧源が交流の場合、つまりVsin wt と書ける場合はいったいどうなるのでしょうか。答えは簡単です。VをVsin wtにすればいいだけです。つまり微分方程式はこのようになります。
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = V \sin(wt)
$$
微分方程式の解き方
まず、前節と同じように
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = 0
$$
の解をまず考えます。前節より解は、
$$
V_C(t) = A \mathrm{e}^{-\frac{t}{RC}}
$$
です。この解を同次解と呼びます。次に定常解を考えます。特殊解を$$ \phi(t) $$とします。特殊解を
$$
RC\,\frac{dV_C(t)}{dt} + V_C(t) = V \sin(wt)
$$
に代入すると特殊解は
$$
RC\,\frac{d \Phi(t)}{dt} + \phi(t) = V \sin(wt)
$$
を満たしていなければなりません。ここで大胆なことをします。$$ \phi(t) = y(t) \mathrm{e}^{-\frac{t}{RC}}
$$
と、同次解の定数部分をあるtの関数に変えたものを定常解として想定します。このような発想で微分方程式を解く方法を定数変化法と呼びます。すると、さっきの方程式は、
$$
RC\,\frac{d y(t) \mathrm{e}^{-\frac{t}{RC}}}{dt} + y(t) \mathrm{e}^{-\frac{t}{RC}} = V \sin(wt)
$$
と書き換えられ、展開すると、
$$
RC \frac{dy(t)}{dt} \mathrm{e}^{- \frac{t}{RC}} + RC y(t) (-\frac{1}{RC}\mathrm{e}^{-\frac{t}{RC}}) + y(t) \mathrm{e}^{- \frac{t}{RC}} = V \sin(wt)
$$
簡単にすると、
$$
\frac{dy(t)}{dt} = \frac{V}{RC} \mathrm{e}^{\frac{t}{RC}} \sin(wt)
$$
この式を両辺をtで積分したらy(t)が求まります。この積分を解説すると長くなってしまうので、演習問題として解いてみてください。
答えは、
$$
y(t) \mathrm{e} ^ {-\frac{t}{RC}} = \frac{V}{1 + (wRC)^{2}} (\sin(wt) – wRC\cos(wt))
$$
です。ただし、Bは積分定数とします。
以上より、この微分方程式の解は、
$$
V_C(t) = A \mathrm{e} ^{-\frac{t}{RC}} + \frac{V}{1 + (wRC)^{2}} (\sin(wt) – wRC\cos(wt))
$$
ですが、定常解の三角関数の部分も加法定理より、定数φを用いることで、
$$
V_C(t) = A \mathrm{e} ^{-\frac{t}{RC}} + \frac{V}{\sqrt{1 + (wRC)^{2}}} \sin(wt + \phi)
$$
と書き換えることができます。ただし、
$$
\tan φ = -wRC
$$
ここで初期条件を $$ V_C(0) = 0 $$ とすると、
$$
A’ = \frac{wRC}{\sqrt{1 + (wRC)^{2}}} V
$$
とわかるので、
$$
V_C(t) = \frac{wRC}{\sqrt{1 + (wRC)^{2}}} V \mathrm{e} ^{-\frac{t}{RC}} + \frac{V}{\sqrt{1 + (wRC)^{2}}} \sin(wt + \phi)
$$
これが答えです。
ただし、十分に時間がたてば定常解の方が同次解よりも優位になります。したがって、この解で最も注目すべきは定常解になります。
答えの物理的解釈
冒頭でも示した通り、この回路は振動します。グラフは以下のとおりです。
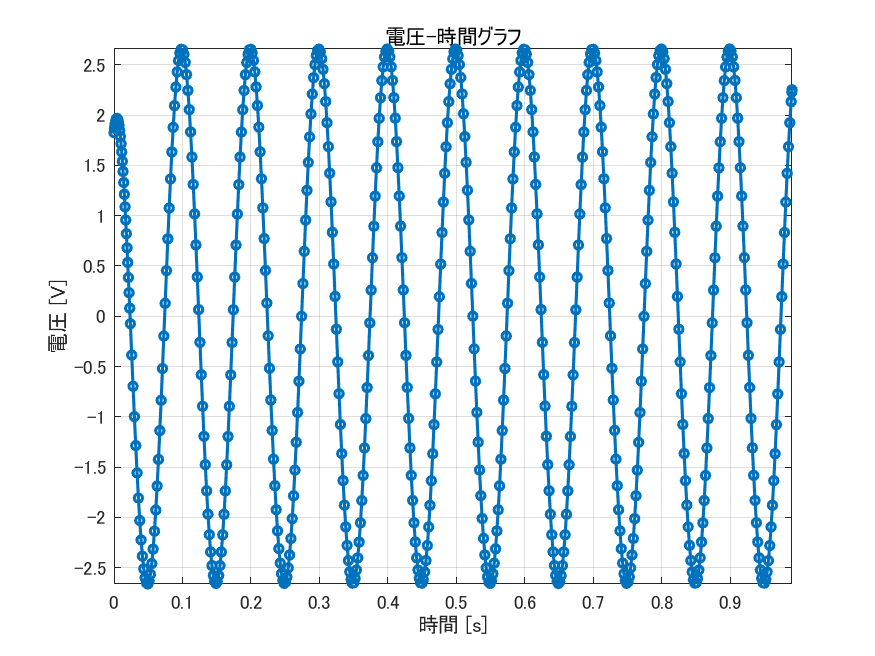
前節で、直流電源なら徐々にコンデンサの電圧が上がり、フル充電されることがわかりました。(参照:RC直列回路からわかる回路の微分方程式)
しかし、交流の場合はフル充電される前に逆の電流が流れることでコンデンサの電圧が下がるわけです。そういうわけでコンデンサの電流はφだけ遅れて交流と同じような波形を描きます。これがコンデンサの特性です。


コメント